 The previous Part I of this essay described the construction of straight-line nomograms using simple geometric relationships. Beyond this, a brief knowledge of determinants offers a powerful way of designing very elegant and sophisticated nomograms. A few basics of determinants are presented here that require no previous knowledge of them, and their use in the construction of straight line nomograms is demonstrated. Then we will see how these determinants can be manipulated to create extraordinary nomograms.
The previous Part I of this essay described the construction of straight-line nomograms using simple geometric relationships. Beyond this, a brief knowledge of determinants offers a powerful way of designing very elegant and sophisticated nomograms. A few basics of determinants are presented here that require no previous knowledge of them, and their use in the construction of straight line nomograms is demonstrated. Then we will see how these determinants can be manipulated to create extraordinary nomograms.
A matrix consists of functions or values arranged in rows and columns, as shown within the brackets in the figure on the right. The subscript pair refers to the row and column of a matrix element. A determinant represents a particular operation on a matrix, and it is denoted by vertical bars on the sides of the matrix. The determinant this 3×3 matrix is given by
a11a22a33 + a12a23a31 + a13a21a32 – a13a22a31 – a11a23a32 – a12a21a33
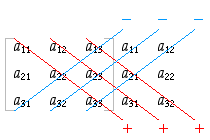 But there are visual ways of deriving it. In the first figure the first two columns of the determinant are repeated to the right of the original, and then the products of all terms on diagonals from upper left to lower right are added and the products of all terms on diagonals from upper right to lower left are subtracted. A convenient mental shortcut is to find these diagonal products by “wrapping around” to get the three components of each term. Here the first product we add is the main diagonal a11a22a33, then the second is a12a23a31 where we follow a curve around after we pick up a12 and a23 to
But there are visual ways of deriving it. In the first figure the first two columns of the determinant are repeated to the right of the original, and then the products of all terms on diagonals from upper left to lower right are added and the products of all terms on diagonals from upper right to lower left are subtracted. A convenient mental shortcut is to find these diagonal products by “wrapping around” to get the three components of each term. Here the first product we add is the main diagonal a11a22a33, then the second is a12a23a31 where we follow a curve around after we pick up a12 and a23 to 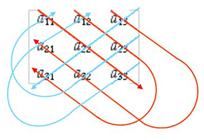 pick up the a31, then a13a32a21 by starting at a13 and wrapping around to pick up the a32 and a21. We do the same thing right-to-left for the subtracted terms. This is much easier to visualize than to describe. Determinants of larger matrices are not considered here.
pick up the a31, then a13a32a21 by starting at a13 and wrapping around to pick up the a32 and a21. We do the same thing right-to-left for the subtracted terms. This is much easier to visualize than to describe. Determinants of larger matrices are not considered here.
There are just a few rules about manipulating determinants that we need to know:
- If all the values in a row or column are multiplied by a number, the determinant value is multiplied by that number. Note that here we will always work with a determinant of 0, so we can multiply any row or column by any number without affecting the determinant.
- The sign of a determinant is changed when two adjacent rows or columns are interchanged.
- The determinant value is unchanged if every value in any row (or column) is multiplied by a number and added to the corresponding value in another row (or column).
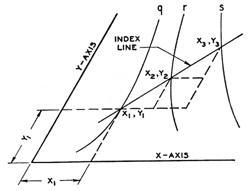 That’s it. Now consider the general diagram to the right from Hoelscher showing three curvilinear scales and an isopleth. Similar triangle relations give
That’s it. Now consider the general diagram to the right from Hoelscher showing three curvilinear scales and an isopleth. Similar triangle relations give
(y3-y1)/(x3-x1) = (y2-y1)/(x2-x1) = (y3-y2)/(x3-x2)
The first two parts of this can be rewritten as a cross product:
(x3-x2) / (y2-y1) = (x2-x1) / (y3-y2)
and when this is expanded it is equal to the determinant equation

We get this result regardless of which pair we choose to use in the cross product. The x and y elements can be interpreted as the x and y values of f1(u), f2(v) and will be f3( w) if we don’t mix variables between rows (the first row should only involve u, etc.) and if the determinant equation is equivalent to the original equation. This is the standard nomographic form. Here y is not expressed in terms of x as we normally have when we plot points at (x,y) coordinates, but rather x and y are expressed in terms of a third variable, that is, x1 and y1 are expressed in terms of a function of the variable u, x2 and y2 are expressed in terms of a function of the variable v, and x3 and y3 are expressed in terms of a function of the variable w. These are called parametric equations. One way to plot them is to algebraically eliminate the third variable between x and y to find a formula for y in terms of x. Another way is to simply take values of the third variable over some range, calculate x and y for each value, and plot the points (x,y)—a more likely scenario when we have computing devices.
Let’s consider the equation (u + 0.64)0.58(0.74v) = w that we used earlier to create a parallel scale nomogram. We converted this with logarithms: to 0.58 log (u + 0.64) + log v = log w + log (0.74), or
0.58 log (u + 0.64) + log v – [log w + log (0.74)] = 0
We could have grouped log (0.74) with any term, but we’ll stay consistent with our earlier grouping. This is an equation of the general form f1(u) + f2(v) – f3( w) = 0, so let’s find a determinant that produces this form. We want each row to contain only functions of one variable of u, v or w, so we’ll start with f1(u) in the upper left corner and 1’s along its diagonal so that the first term of the determinant will be f1(u).

Now let’s set the lower left corner to f3( w) and the upper right corner to 1 so the last term of the determinant will be –f3( w):
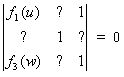
Now we can place f2(v) in the middle row somewhere and fill in the rest of the determinant so the terms involving these elements end up simply as f2(v). Here are a few possibilities that work:
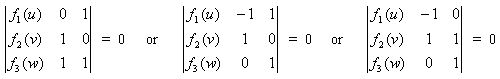
But the second determinant is simply the first one after the third column is subtracted from the second column and the third determinant is simply the second one after the third column is added to the second column. These are operations that will not change our determinant equation as described in our earlier list, so they are all equivalent.
Now we want the flexibility to scale our f1(u) and f2(v) by m1 and m2 calculated for parallel scale charts as the desired height of the nomogram divided by the ranges of the functions. If we take the first determinant of the three possible ones shown, notice that we can introduce the scaling values without changing the determinant equation if we write it as

So now we have to convert this to the standard nomographic form having all ones in the last column (and continuing to isolate variables to unique rows). First we add the second row to the third row, where 1/m1 + 1/m2 = (m1+m2)/m1m2:

Then we multiply the bottom row by m1m2/(m1+m2) and swap the first two columns so that the y column (the middle column) contains the functions:
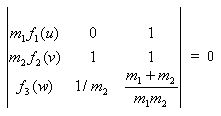
and we have the determinant in standard nomographic form. The first column represents x values and the second column represents y values of the functions. The scaling factors of m1 and m2 result in a scaling factor m3 for the w-scale of m1m2/(m1+m2) as we found earlier from our geometric derivation. We had calculated m1 = 25.72 and m2=19.93 before, giving m3=11.23. This determinant also shows that we place the u-scale vertically at x=0 and the y-scale vertically at x=1, with the w-scale at x= m (m1+m2) = 0.5634, but in fact we can multiply the first column by 3 to get a scale of 3 inches, and in this case the w-scale lies vertically at x=1.69 inches, and so we end up with exactly the same nomograph we found in Part I using geometric methods.
This was a bit of work, but we have found a universal standard nomographic form for the equation f1(u) + f2(v) – f3( w) = 0 including scaling factors.
Let’s derive a Z chart for division using determinants. For v = w/u, we rearrange the equation so the right-hand term is 0, or uv – w = 0. One possible determinant we can construct is
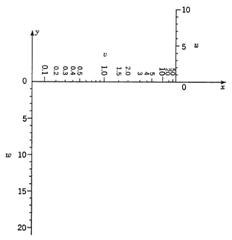

which graphs to the nomogram on the right, a Z chart with a perpendicular middle line. A different determinant would result in a Z chart of the more familiar angled middle line. An interesting aspect of such a chart is that the u-scale and v-scale have different scaling factors despite the fact that they can be interchanged in the equation.
There is a definite knack to all of this, and at this point I’d like to recommend the webpages on nomography by Winchell D. Chung, Jr. at this site. His webpages are quite interesting to read—there are quite a few examples of nomograms, and the determinant approach is used throughout. In particular, he provides other examples of expressing an equation into determinant form here. He also gives a few examples of converting the determinant to the standard nomographic determinant form here, where examples 2 and 3 are from Hoelscher. Most importantly, for equations of several standard formats Chung also reproduces tables that map these equations directly to standard nomographic determinant forms here.
Determinants are most useful when one or more of the u, v and w scales is curved. The quadratic equation w2 + uw + v = 0 can be represented as the first equation below, and dividing the last row by w-1 we immediately arrive at the standard nomographic form shown in the second equation:
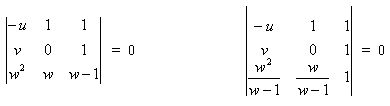
 The u-scale runs linearly in the negative direction along the line y=1. The v-scale runs linearly in the positive direction with the same scale along the line y=0. The x and y values for the curve for w can be plotted for specific values of w (a parametric equation), or w can be eliminated to express the curve in x and y as
The u-scale runs linearly in the negative direction along the line y=1. The v-scale runs linearly in the positive direction with the same scale along the line y=0. The x and y values for the curve for w can be plotted for specific values of w (a parametric equation), or w can be eliminated to express the curve in x and y as
x/y = w
y = (x/y) / [(x/y) – 1] = x / (x – y)
resulting in the figure at the right in which the positive root w1 of the quadratic equation can be found on the curved scale (the other root is found as u – w1).
Hoelscher presents the equation for the projectile trajectory Y = X tan A – gX2 / (2V02cos2A) where A is the initial angle, V0 is the initial velocity, and g is the acceleration due to gravity. There are four variables X, Y, V0 and A, so nomographic curves are plotted for different values of A. For an angle of 45º, the equation reduces to
Y = X – 0.0322X2 /V02
One determinant for this is shown in the first equation below, which can be manipulated into the standard nomographic form shown in the second equation:
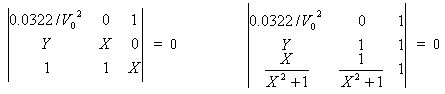
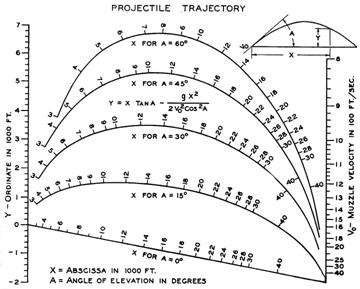 Hoelscher assumes -2000<Y<7000 ft and 800<V0<4000 fps and a chart of 5 inches square, so after some more manipulations (including the swapping of the first two columns) we arrive at the final form:
Hoelscher assumes -2000<Y<7000 ft and 800<V0<4000 fps and a chart of 5 inches square, so after some more manipulations (including the swapping of the first two columns) we arrive at the final form:
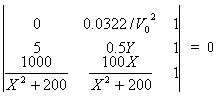
This is shown as the curve for A=45º along with curves for other angles in this figure (a grid nomogram such as this can be used to handle an equation with more than 3 variables).
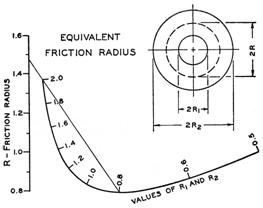
It’s possible to have two or three scale curves depending on how the determinant works out, and it is possible to have two or all three curves overlap exactly. The equation for the equivalent radius of the friction moment arm for a hollow cylindrical thrust bearing is R = 2/3 [R13 – R23] / [R12 – R22] or 3RR12/2 – 3RR22/2 – R13 + R23 = 0, yielding the determinant
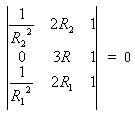
Here the R1 and R2 scales lie exactly on the same curve. They could have separate tick marks on this curve if they had a different scale, but here they have the same scaling factor. The figures here show the plotted nomogram for perpendicular x and y axes, and also for oblique axes that expand the R-scale to the full height of the nomogram for greater accuracy.

Otto provides an interesting alternate determinant for the equation f1(u) + f2(v) + f3( w) = f1(u) f2(v) f3( w).
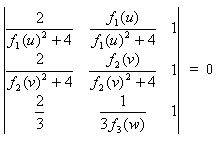
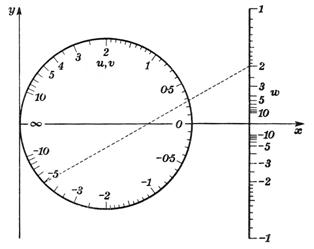 The nomogram for the particular equation of this type u + v + w = uvw is shown in this figure, where again two of the three scales overlap. Eliminating f1(u) from the x and y elements in the first row we find that u lies along the circle given by (x – ¼)2 + y2 = 1/(42), and this is correspondingly true for v as well (although in general we have to separately calculate x and y tick marks based on f1(u) or f2(v) values).
The nomogram for the particular equation of this type u + v + w = uvw is shown in this figure, where again two of the three scales overlap. Eliminating f1(u) from the x and y elements in the first row we find that u lies along the circle given by (x – ¼)2 + y2 = 1/(42), and this is correspondingly true for v as well (although in general we have to separately calculate x and y tick marks based on f1(u) or f2(v) values).
Finally, Otto describes a very interesting determinant that can be created for the equation f1(u) f2(v) f3( w) = 1.
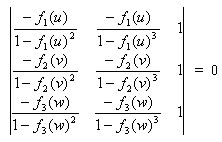
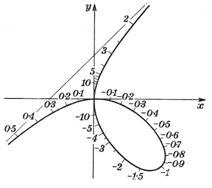
 For uvw=1, all three scales coincide and have the same scaling factor, and it turns out that the equation for this curve is x3 + y3 – xy = 0 (called the folium of Descartes). This nomogram is shown as the curled figure to the right.
For uvw=1, all three scales coincide and have the same scaling factor, and it turns out that the equation for this curve is x3 + y3 – xy = 0 (called the folium of Descartes). This nomogram is shown as the curled figure to the right.
Determinants provide a creative way of generating nomograms whose designs are varied and interesting. We can also apply transformations to the x and y elements of the determinants to morph nomograms into shapes that are most accurate for given ranges of the variables or that utilize the available space most efficiently (or are simply more pleasing to the eye). Transforming nomograms is the subject of Part III of this essay.
<<< Back to Part I of this essay >>> Go to Part III of this essay
Here’s a possibly-helpful thought about why the determinant works.
Normally, determinant = 0 is used as a rule for detecting when a set of vectors based at the origin doesn’t span the whole space. So, for points in a plane, normally you’d have a 2×2 determinant that detects whether two points are collinear with the origin, but here we have a 3×3 determinant that detects whether three points are collinear with each other, not including the origin. So what’s going on? The trick is to take that third column seriously and read it as the z coordinate of the points. Three points in the plane z=1 are collinear with each other if and only if they’re coplanar with the three-dimensional origin … and that’s exactly what a 3×3 determinant detects.
Very interesting—I haven’t seen this explanation anywhere and it’s a really neat way to conceptualize why the standard nomographic form works. Thanks, John. — Ron
LikeLike
Very excited seeing this. I took a course in nomography in 1961. It still works!
Thanks, Ron – Paul
You’re quite welcome. I’m really gratified by the interest people are showing in this arcane field. — Ron
LikeLike
Ron,
I took a course in nomography in 1967. I ended up doing my master’s thesis in the area “A Nomographic-Electronic Computer with a Random Access Memory” (June 1972). Basically, I set up the three curves as six tables in RAM one each for x and y indexed by the scaled parameters. I interpolated the values in two sets of tables to get x1, y1, x2, and y2 then searched along the line formed by (x1,y1)-(x2,y2) for the intersection with the curve specified by the third set of tables, x3 and y3.
Best wishes,
–Phil
Thanks, Phil. I am continually amazed at the history that people have with nomography, a subject I’ve only encountered in the recent past.
The intersection of two technologies seems to bring out the most creative activities. Are you familiar with Chapter 14 (Appendix D) of Adam’s “Nomography: Theory and Application” in which he describes something along the same lines but using an optical reader and counters rather than RAM? He uses the same term, “Nomographic-Electronic Computer” or NOEL, and I gather from the bibliography he provides (which ends in 1963 when he wrote the book) that this was quite an active field of mathematical research. BTW, this book by Adams is my favorite one on nomography, really original and eye-opening.
Thanks again for contributing to the blog. I know from emails I receive that people find the comments at least as interesting as the essays. — Ron
LikeLike
I studied under Professor Douglas P. Adams fifty years ago exactly and wrote a paper for him exploring his idea of spinning and summing across a film dotted with coordinate bits and variable bits. Another student as I recall actually built the circuits required. I was intrigued as I had written Univac I programs to test the FOSDIC device designed to translate census form blackened spots onto unitape for census processing (“film operated sensing device for input to computers”). In my subsequent career writing software for computer manufacturers and small and large businesses I never had to address the engineering calculations addressed by this kind of logic. Only in my recent study of robotics do I see how useful this device might have been, in the early days of Moore’s law. Now all that’s left is the beauty.
In another class that year I was warmly warned that there are always two ways of calculating – figuring, and asking: data lookup. The mechanics of looking up (by counting) a nomographic calculation beautifully blend the processes without denying their philosophically separate identities.
Thanks, Bill—recollections like yours are very interesting to me. As I’ve poked around the Internet I’ve come across works of Dr. Adams online, including papers and patents. Meanwhile, his book on the used market has gotten quite expensive! — Ron
LikeLike
Hi Bill,
As I mentioned to Ron, I did my Master’s Thesis under Professor Adams in 1972. I used TTL logic and (simulated) RAM lookup to replace the counting processes used in earlier versions of Nomographic-electronic computers.
BTW, I Googled “nomographic electronic” and got some interesting hits including a summary of Professor Adam’s report of a study done for the Air Force
Click to access GetTRDoc
Best wishes,
–Phil Martel
LikeLike
I was introduced to nomograms and determinants by my uncle in about 1950. He was responsible for water purification in the then Gold Coast and developed a set of simple lab routines to calculate the dosages of chemicals for optimum treatment. These involved nomograms, which were drawn to a large scale, printed, waterproofed, and hung on the wall of lab with an attached piece of string. The result was a HMSO monograph describing the whole systems.
Unfortunately, I no longer have the monograph he gave me, but it appears that I may need to brush up the subject for a lecture in the maths colloquium of our local U3A (“University of the Third Age”). Your site will be an excellent starting point.
The first and simplest example was deriving the correct jet size for Aluminium sulphate treatment to effectively precipitate suspended colloids without leaving an excess in the output. (shades of Camelford)
Wow, I hadn’t heard of the Camelford incident before and I was shocked when I Googled it and read about the massive water supply contamination with aluminium sulphate! What a disaster. (I also had not heard of U3A until I looked it up—I must really be out of touch.) I hope you are able to reconstruct the basis for the nomograms. If you have questions or need any help, feel free to contact me. — Ron
LikeLike
Douglas P Adams was my father’s cousin so, I guess, mine too. I knew him well. I introduced a fellow engineer to him as he was pursuing mathematical analyses of 4 bar linkages and Doug was interested in nomographic solutions. I felt that if I knew 2 people interested in this esoteric subject it was my obligation to acquaint them. Years later I met my friend and he said that introduction changed his life as Doug inspired him to teach part time. Doug passed away suddenly in the late ’70s. Recently the family has been uncovering letters between Doug and my late father which reveal much about their early years growing up poor but undaunted in Charlestown, MA.
Mr. Adams is still an influence on me with his excellent book, patents and articles on nomography. In fact, I recently created my first totally circular nomograms (for an essay I’m working on) based on an article he co-wrote in 1948. The article can be found here and I’ve extracted my two circular nomograms from the essay in progress so you can see what they look like here. (Computing mechanisms based on linkages will be the subject of an essay at some point in the next year.) Thanks, John. — Ron
LikeLike