The final completion of my 2013 calendar, Graphical Astronomy, has been delayed, so at this point I am going to update the dates for 2014 and post it this fall. As partial compensation, I’ve created a Valentine’s Day card for mathematically-inclined people that can be downloaded, printed and folded. It is appropriate whether the person giving the card or receiving it is interested in math, or both, and in fact it’s not Valentine’s Day specific so it can be used for birthdays or anytime at all.
mathematics
Bayes’ Theorem, Medical Diagnostics and Nomograms
Last month Joe Marasco, Leif Roschier and I published an article on Bayes’ Theorem in The UMAP Journal that included a foldout of large circular nomograms for calculating the results from it. The article, Doc, What Are My Chances?, can be freely downloaded from the Modern Nomograms webpage, which also offers commercial posters of the two nomograms used to calculate Bayes’ Theorem (one for common cases and one optimized for calculating rare cases).
New Modern Nomograms Website
I want to announce that my fellow collaborators in nomography, Joe Marasco and Leif Roschier, and I have a new website called Modern Nomograms to offer posters of new nomograms that we hope will interest people. Our initial posters are nomograms for calculating results from Bayes’ Theorem as described in the next post here, but we expect more will follow.
This project does not in any way affect the content here—essays will continue to be written as usual on lost arts in the mathematical sciences, including nomography. This is simply an outlet to provide an option for nomograms in poster form.
The 13th Root of a 100-Digit Number (Part II)
by Ron Doerfler and Miles Forster
Part I of this essay provided background information that demonstrates the difficulty of the problem of mental extraction of 13th roots and the efforts of calculators to master it. But can it be possible for us to extract 13th roots of 100-digit numbers without devoting portions of our life to it? With a basic talent in mental arithmetic and some study, it can certainly be done, even if not in record time. We present a new method that involves no logarithms, no antilogarithms and no factoring, one that works with 13th powers that end in 1, 3, 7 or 9 (the cases attempted by record holders). The memorization consists of one table and a few formulas. A printer-friendly PDF version of Parts I and II is linked at the end of this essay.
The 13th Root of a 100-Digit Number (Part I)
by Ron Doerfler and Miles Forster
Mental calculators of note (so-called “lightning calculators”) developed areas of expertise in performing calculations that seem astonishing, even unbelievable, to the rest of us. One such specialty is calculating the 8-digit root of a 13th power of 100 digits. Achieving record times historically required massive memorization and calculating speed, racing through a procedure that remains a mystery to most people. Part I of this essay provides a historical overview of the extraction of 13th roots, including the methods used by a few mental calculators, methods that largely rely on a mix of intensive mental calculation and large-scale rote memorization. It demonstrates the creativity and drive of these marvelous people.
In Part II of this essay we will propose a new method for 13th roots like those posed to lightning calculators that is relatively easy to learn, one that makes this feat feasible for those of us with basic mental math capabilities and a desire to do something amazing. A printer-friendly PDF version of Parts I and II is linked at the end of this essay.
Book Review: The History and Development of Nomography, by H.A. Evesham
Those of us who enjoy our expeditions through the lost world of nomography quickly discover that many original sources that are still considered masterpieces in the field have never been translated into English. In my case this is a serious handicap, and I find myself struggling through the texts trying to understand the rationale behind the beautiful nomograms I see on the printed page. Nomography and its predecessors were invented in France and only later spread to such places as Germany, the U.S, Britain, Russia and Poland. Today it seems to me that most research appears in Czech journals. In addition to the language difficulties, many of the original sources are in obscure, hard-to-find journals.
In 1982 H.A. Evesham produced his doctoral thesis, a review of the important discoveries in nomography. It is often cited in other works, but unless you know someone who knows someone, it is very difficult to find—I have never been able to locate a copy. However, just recently Mr. Evesham’s thesis has been professionally typeset and released as a book (click here or here) by Docent Press under the aegis of Scott Guthery. If you have an interest in the theoretical aspects of nomography beyond the basic construction techniques of most books and of my earlier essays, you will appreciate this book as much as I do. Mr. Evesham does a wonderful job of weaving mathematical discoveries in nomography from many contributors into a readable but scholarly work.
A 2011 “Lightning Calculation” Calendar
I have researched and written about methods of mental calculation over the years, and I’m often surprised at the ingenuity evident in the mathematical methods developed specifically for it. Based on my Lightning Calculator series of essays here, I’ve created a new 2011 calendar titled Lightning Calculation. It’s a unique, interactive calendar for developing abilities in mental calculation. You can download a free PDF file for printing on your computer, or if you prefer, order it for delivery through Lulu.com. I also think it might be a nice thing to make as a Christmas gift for someone interested in this sort of thing, or for displaying in a math classroom.
Lallemand’s L’Abaque Triomphe, Hexagonal Charts, and Triangular Coordinate Systems (Part II)
Part I of this essay described and analyzed Charles Lallemand’s L’Abaque Triomphe, the first published example of a graphical computer called a hexagonal chart. Here we discuss the mathematical principles behind hexagonal charts and provide examples of these charts from the literature of the time. The related development of triangular coordinate systems is also covered in this second part. Trilinear diagrams, a simpler offshoot of triangular coordinate systems, are still seen today in fields such as geology, physical chemistry and metallurgy (as shown to the left). A list of references is provided as well. A printer-friendly Word/PDF version with more detailed images is linked at the end, with a hexagonal overlay in the appendix that can be used to exercise these charts.
Lallemand’s L’Abaque Triomphe, Hexagonal Charts, and Triangular Coordinate Systems (Part I)
In 1885, Charles Lallemand, director general of the geodetic measurement of altitudes throughout France, published a graphical calculator for determining compass course corrections for the ship, Le Triomphe. It is a stunning piece of work, combining measured values of magnetic variation around the world with eight magnetic parameters of the ship also measured experimentally, all into a very complicated formula for magnetic deviation calculable with a single diagram plus a transparent overlay. This chart has appeared in a number of works as an archetype of graphic design (e.g., The Handbook of Data Visualization) or as the quintessential example of a little-known graphical technique that preceded and influenced d’Ocagne’s invention of nomograms—the hexagonal chart invented by Lallemand himself. Here we will have a look at the use and design of this interesting piece of mathematics history, as well as its natural extension to graphical calculators based on triangular coordinate systems. Part I of this essay covers Lallemand’s L’Abaque Triomphe, while Part II covers the general theory of hexagonal charts and triangular coordinate systems. A printer-friendly Word/PDF version with more detailed images is linked at the end of the essay.
Nomography Article in the UMAP Journal
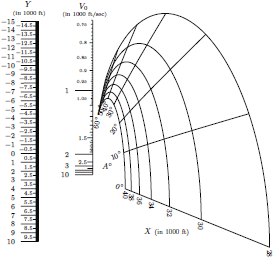Last summer a fellow nomography enthusiast and friend, Joe Marasco, e-troduced me to the editor of the Undergraduate Mathematics and Its Applications (UMAP) Journal, with the idea of submitting my original 3-part nomography essay on this blog for publication. The experience I’ve had on this project with Paul Campbell, a professor at Beloit College and the editor of the journal, has been superb. In addition to his enthusiastic support on the article, he invited me to give talks on nomography and sundials at the college, which I thoroughly enjoyed doing last September.
The article, a significantly revised version of my blog essay, has now been published in the UMAP Journal, and per the standard agreement I can post the PDF of the article here for anyone to download. More information and a link to the article are below.
Dead Reckonings 